5.7. RANSAC Paradigm
The RANSAC plgorithm was first introduced by Fischler and Bolles in [FischlerBolles1981].
5.7.1. Video
This is a nice explanation by Behnam Asadi from YouTube.
5.7.2. RANSAC is Not Least Trimmed Squares
Typically in Least Squares (LS) fitting, we use all the data to fit a model.
In Least Trimmed Squares, you compute LS, throw away a percentage of bad data, then recompute, and repeat.
Fischler and Bolles show, this can still fail, as the initial model can be affected by the bad data.
They wanted a more robust method.
5.7.3. The Paradigm
Given a model that requires a minimum of 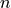 points to compute a solution,
and a set of data points
points to compute a solution,
and a set of data points 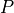 where
where 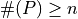 :
:
Select a random subset of
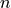 data points from
data points from 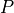 to form
to form 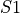
Instantiate the model
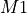
Determine the set
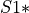 within error threshold of model
within error threshold of model 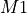 , and count the members of
, and count the members of 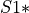 . This is the consensus set.
. This is the consensus set.If
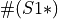 greater than a threshold
greater than a threshold 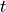 , use
, use 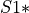 to compute a new model
to compute a new model 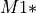
If
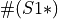 is less than
is less than 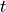 , select a new random subset
, select a new random subset 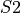 and repeat.
and repeat.If after
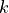 iterations, no consensus set with
iterations, no consensus set with 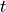 or more members has been found, solve with the largest consensus set, or terminate with failure.
or more members has been found, solve with the largest consensus set, or terminate with failure.
Parameters:
 : error threshold to determine which points are inliers
: error threshold to determine which points are inliers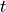 : minimum number of inliers to accept as forming a valid model
: minimum number of inliers to accept as forming a valid model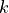 : number of iterations to try
: number of iterations to try
Referring to paper:
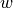 : probability that any given point is within error tolerance of model
: probability that any given point is within error tolerance of model : certainty that at least one of our subsets contains error free data
: certainty that at least one of our subsets contains error free data
So,
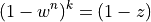
gives:
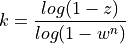
For example, if we think that 20 percent of the data is bad, the probability of picking a good data point
is 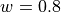 . If we want 99 percent confidence that we will end up with a good model then,
. If we want 99 percent confidence that we will end up with a good model then,
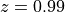 . So, in a line fitting problem,
. So, in a line fitting problem, 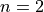 , so the number of iterations
, so the number of iterations 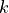 we should
attempt should be:
we should
attempt should be:
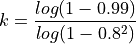
which is 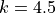 , so at least 5 iterations should be made.
, so at least 5 iterations should be made.
Alternatively, the paper derives the expectation of 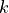 as:
as:
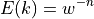
and the standard deviation of 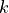 to be:
to be:
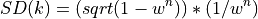
which in the same example gives, a mean of 1.56, a SD of 0.9, so if we wanted mean plus 3 standard deviations, its we’d need 5 iterations again.
With poor data, say 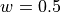 , we’d need approx 16 iterations.
, we’d need approx 16 iterations.
From [FischlerBolles1981], you could terminate early the first
time you get a consensus set larger than a minimum size, i.e. threshold 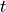 ,
or if you don’t get over
,
or if you don’t get over 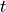 , just pick the largest consensus set you found.
, just pick the largest consensus set you found.
It depends if you want to finish early, or fit the most data, so in practice, implementations may differ.
For another explanation, see Ziv Yaniv’s example, which uses RANSAC to solve for parameters of a hyperplane and hypersphere, and discusses various implementation details.
5.7.4. Widely Applicable
It’s not a specific algorithm
It’s a way of solving model fitting problems
So, problem and implementation specific
e.g. Pivot calibration, pose estimation, line fitting
5.7.5. Notebooks
Have a play with the provided Jupyter Notebooks.
scikit-surgery provides the main algorithms:
# Note that the scikit-surgery libraries provide pivot and RANSAC.
import sksugerycalibration.algorithms.pivot as p # AOS Pivot algorithm and a RANSAC version.
import sksurgerycore.transforms.matrix as m # For creating 4x4 matrices.
so the algorithms are here and the matrix utilities are here.
and can be installed with:
pip install scikit-surgerycalibration