# Jupyter notebook sets the cwd to the folder containing the notebook.
# So, you want to add the root of the project to the sys path, so modules load correctly.
import sys
import matplotlib.pyplot as plt
import numpy as np
sys.path.append("../../")

Monte Carlo Simulation

Mostly based on YouTube video: https://youtu.be/slbZ-SLpIgg?si=JEZA-BJsM8vEuD4b

From lecture slides:

• Identify input parameters and distributions based on realistic estimates

• Sample from random distribution

• Compute output result

• Repeat X number of times from step 2

• Analyze output variable, e.g. mean, std-dev, probability of success?

• Repeat whole experiment Y times to get confidence in intervals.

1. Create Model.

Convert “We want 2 reports by end of day” into some kind of model, with an appropriate distribution. As per the video, we are going to model the time taken to write a report by a uniform distribution. So, time to complete the reports A and B is equiprobable between the low and high limits.

A = np.random.uniform(low=1.0, high=5.0, size=1)
B = np.random.uniform(low=2.0, high=6.0, size=1)
duration = A + B
print(f"One sample is A={A}, B={B}, duration={duration}")

One sample is A=[4.65451823], B=[4.58680826], duration=[9.24132649]

If you re-reun the above cell, you will get a different number each time you run it.

2. Sample from Distribution X Times, Compute Output.

Depending on your programming style, you can for example

• Use a for loop, to sample each number, and compute model inside loop.

• Or use array arithmetic, which should be slightly faster.

• (or some other programming style)

# This variable controls the number of samples.
sims = 100000

# Option 1: Using for loop. Slow, but might be easier to follow.
duration_samples = []
for i in range(0, sims):
    A_sample = np.random.uniform(low=1.0, high=5.0, size=1)
    B_sample = np.random.uniform(low=2.0, high=6.0, size=1)
    duration_sample = A_sample + B_sample
    duration_samples.append(duration_sample)

print(f"Using loop: mean={np.mean(duration_samples)}, std_dev={np.std(duration_samples)}")

Using loop: mean=7.000179151940462, std_dev=1.6340022165497035

# Option 2: Using arrays. Faster, but depending on the complexity of model, may be confusing.
A_samples = np.random.uniform(low=1.0, high=5.0, size=sims)
B_samples = np.random.uniform(low=2.0, high=6.0, size=sims)
duration_samples = A_samples + B_samples
print(f"Using arrays: mean={np.mean(duration_samples)}, std_dev={np.std(duration_samples)}")

Using arrays: mean=6.994243848803083, std_dev=1.6353599457753278

Analyse Output.

This does depend on the specific problem you are studying. You could compute

• some summary statistics, e,g. mean, standard deviation of total time taken.

• probability of total time being too much (in this case, being late for the party. i.e. total time > 9 hours.)

plt.figure(figsize=(3, 1.5))
plt.hist(duration_samples, density=True)
plt.axvline(9, color='r')
plt.show()
print(f"Probability of going over 9 hours:{(duration_samples > 9).sum() / sims}")

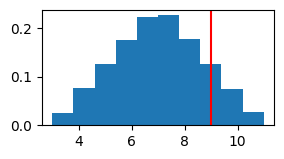
Probability of going over 9 hours:0.12318

Confidence Limits.

Imagine the scenario above was done with only 1, 2, or say 10 samples for the length of each report? Would it be a good thing to reply on the probability derived. It may be the case that the small number of samples, say 1, 2, or 10, gave exactly the right answer. But it may also be the case that we just got lucky/unlucky with the data, and we predict say 12.5 %, when in reality the unknown true value is different. What we want is a measure of certainty or “confidence” in the prediction. We want to be able to say, “The expected total time is X, and I’m Y (say 95%) confident that my estimate lies within a range A-B”.

Confidence Intervals by Empirical Rule

# Method 1: Assuming normally distributed output value (duration of time in this case). Use "Empirical Rule"

# i.e. You hard code the rule from standard lookup tables:
# 68% of data within 1.0 std dev.
# 95% of data within 1.96 std dev.
# 99.7% of data within 3 std dev.

mean_of_total_times = np.mean(duration_samples)
std_dev_of_total_times = np.std(duration_samples)
low = np.round(mean_of_total_times - 1.96 * std_dev_of_total_times, 2)
high = np.round(mean_of_total_times + 1.96 * std_dev_of_total_times, 2)

print(f"Expected total time is {np.round(mean_of_total_times,2)}, and I'm 95% confident that the total time will lie within {low} and {high} hours.")

Expected total time is 6.99, and I'm 95% confident that the total time will lie within 3.79 and 10.2 hours.

Confidence Intervals by Simulation

The Empirical Rule is valid when the mean estimation error is zero. i.e. no inherent bias either way. This is normally a reasonable assumption in modelling, but may not be valid in a practical experiment, e.g systematic measurement error. The second assumption that the Empirical Rule makes is that the errors are normally distributed (i.e. Gaussian). This means you are fitting (or assuming) a Gaussian model to the data (a measure of time), and making predictions based on that assumption.

Alternatively you can also estimate the confidence intervals, directly from the data.

low = np.round(np.percentile(duration_samples, 2.5), 2)
high = np.round(np.percentile(duration_samples, 97.5), 2)
mean_of_means = np.round(np.mean(duration_samples), 2)
print(f"Expected total time is {mean_of_means}, and I'm 95% confident that the total time will lie within {low} and {high} hours.")

Expected total time is 6.99, and I'm 95% confident that the total time will lie within 3.88 and 10.11 hours.

Quality of Confidence Intervals

So the quality or reliability of the confidence intervals are determined by:

• For the Empirical Rule - whether the data has zero mean errors and the errors are normally distributed

• For the Simulation - whether there are enough samples to be a realistic representation

Questions To Play With

• In the example above, we are using a uniform distribution. As the number of trials (sims variable) goes up, will the confidence interval shrink? If not, why not?

• What happens if you switch Uniform distributions to Normal distributions in the above model?

• Can you put a confidence interval on a probability? (i.e. you want an answer like: “The model estimates there is an expected X% chance of going over 9 hours, and we can be 95 on that percentage is between A